No Brasil, 50% dos casos de influenza registrados já se devem ao vírus H1N1, segundo boletim divulgado em 4 de maio pelo Ministério da Saúde. Isso preocupa as autoridades sanitárias, pois esse subtipo é mais agressivo do que os demais vírus da gripe que circulam no país. Em termos estatísticos, duas variáveis são consideradas críticas para o enfrentamento exitoso de uma epidemia: o tempo de detecção da doença e o tempo de isolamento dos indivíduos afetados. Um modelo criado no Centro de Ciências Matemáticas Aplicadas à Indústria (CeMEAI) – um Centro de Pesquisa, Inovação e Difusão (CEPID) financiado pela FAPESP – definiu a equação que permite calcular o valor ótimo para o tempo de detecção.
O estudo faz parte do trabalho de doutoramento de Stefan Ruschel, da Humboldt-Universität, na Alemanha. Orientado por Serhyi Yanchuk, em Berlim, Ruschel está concluindo seu doutorado no Brasil, sob orientação de Tiago Pereira, professor do Instituto de Ciências Matemáticas e de Computação da Universidade de São Paulo, no campus de São Carlos, e pesquisador do CeMEAI.
O trabalho é apoiado por meio do acordo de cooperação da FAPESP com o Deutsche Forschungsgemeinscharf (DFG), no contexto do Projeto Temático “Fenômenos dinâmicos em redes complexas: fundamentos e aplicações”.
“Partimos de um modelo clássico da epidemiologia, o Susceptible – Infectious – Susceptible (SIS), que descreve infecções como as causadas pelos vírus da influenza, que não conferem imunização duradoura às pessoas que as contraem e se recuperam”, disse Pereira à Agência FAPESP.
“Os indivíduos são suscetíveis antes, infectados durante e suscetíveis depois. Esse modelo considera, portanto, apenas dois estados: ou as pessoas estão saudáveis ou as pessoas estão doentes. Nossa ideia foi agregar um terceiro estado: os indivíduos isolados. No novo modelo, os indivíduos infectados são identificados após um certo tempo e isolados para o tratamento”, disse.
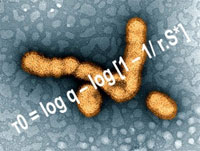
Com base nessa reconfiguração do modelo, os pesquisadores chegaram à equação τ0 = log q – log [1 – 1/ r.S*], na qual τ0 é o tempo de detecção e diagnóstico da doença; q, a fração da população infectada identificada; r, o número de pessoas que podem ser infectadas se tiverem contato com um indivíduo já infectado (esse número varia de acordo com a enfermidade); e S*, a fração de indivíduos saudáveis na população.
“Se a doença for diagnosticada em tempo menor ou igual a τ0, o isolamento será sempre efetivo. Mas, se a doença for diagnosticada em tempo maior do que τ0, o sucesso na erradicação passará a depender criticamente do tempo de isolamento”, explicou Pereira.
Assumindo que tivesse sido possível identificar todos os indivíduos infectados (q = 1) e controlar completamente a doença (S* = 1), os pesquisadores obtiveram para algumas epidemias analisadasos seguintes tempos críticos de detecção:
– Gripes sazonais: r aproximadamente igual a 1,2, portanto, τ0 = 5,4 dias
– Gripe Espanhola em 1917: r aproximadamente igual a 2; portanto, τ0 = 2,1 dias
– Ebola em 2014 (Guiné e Libéria): r aproximadamente igual a 1,5; portanto, τ0 = 3,3 dias
– Ebola em 2014 (Serra Leoa): r aproximadamente igual a 2,5; portanto, τ0 = 1,6 dia
Nesse tipo de cálculo, a população de um país é considerada um conjunto fechado – isto é, sem entradas e saídas de indivíduos. É claro que se trata de uma situação ideal, que não se aplica ao quadro real da epidemia de H1N1 no Brasil, onde as fronteiras estão abertas e a doença já se encontra disseminada em uma grande parcela da população. Mas a equação pode ajudar as autoridades de saúde a definir estratégias para o enfrentamento de epidemias futuras.
Agência FAPESP
